Similarities between simulating a single cell and the entire universe
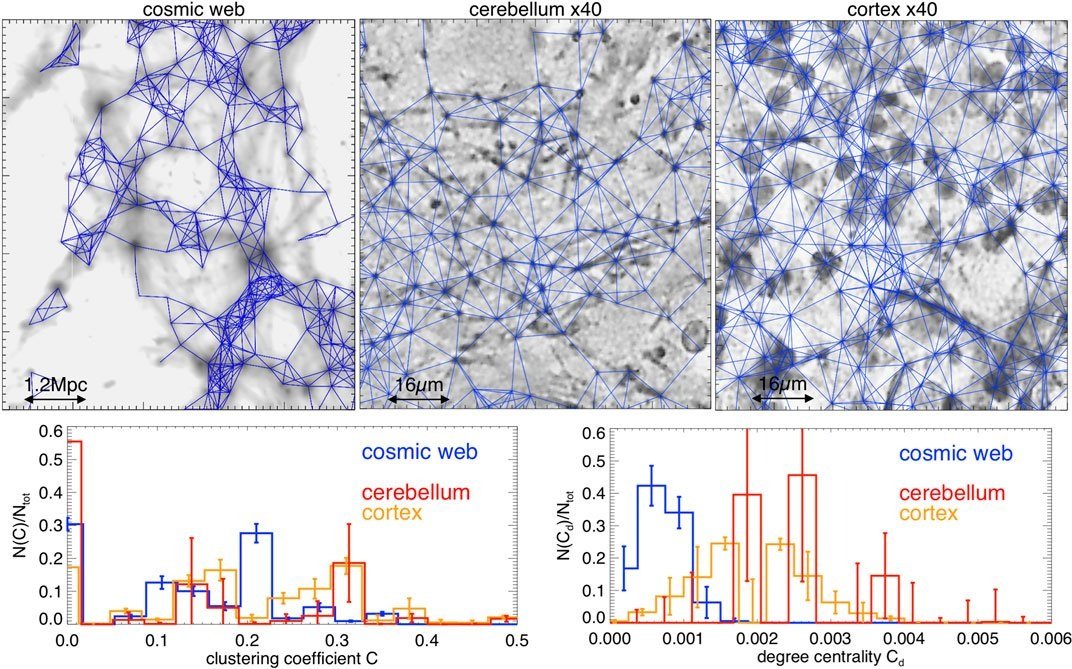
Figure 3 from Vazza and Feletti 2020, showing quantitative similarities between the cosmic web and neuronal networks.
While biological cells are admittedly quite a bit smaller than the entire universe, I recently found myself reflecting on the similarities between the two. By no means am I the first to do so. In fact, one recent(ish) paper even made quantitative comparisons between the structure of the entire universe (the “cosmic web”) and networks of neurons in the human brain (Vazza and Feletti 2020).
My thoughts were elicited by listening to Sean Carroll’s conversation with Andrew Pontzen, a computational cosmologist. On Dr. Carroll’s podcast, Mindscape, they conversed about the art of constructing simulations of the evolution of the cosmos, including strange participants such as dark matter and dark energy (and normal matter and energy, which can be oddballs themselves). I myself spend my time thinking about implementing computational physical models, but at a much much smaller scale (about 32 orders of magnitude smaller than the observable universe). I use such models to examine objects with incredibly detailed structure and an astounding level of electrical, chemical, and mechanical complexity - the biological cell. Using a few of the themes discussed in the podcast episode and in Dr. Pontzen’s new book, The Universe in a Box, I would like to the importance of computational modeling across these extremely different scales of length and time.
1. The necessity and art of the sub-grid: I don’t remember hearing the term “sub-grid” before listening to this episode and reading the book, but it encapsulates an idea I am quite familiar with from my own modeling efforts - when modeling a complex system like a biological cell, the weather, or the universe, we have little hope of capturing every single detail down to the single molecule scale. Rather, we coarse-grain these systems and model them at some chosen level of detail, be it mixtures of molecules, clusters of clouds, or clusters of galaxies. But, an issue arises - the phenomena we want to simulate at this higher level are intrinsically tied to events at the lower level, or in the “sub-grid” (smaller than the resolution of the simulation). You may think that this is not an issue when modeling cells, but to the contrary, a single cell contains on the order of 100 trillion atoms. Some of the largest simulations that capture “single-atom” level detail can simulate just over 1 billion atoms, capturing about 10 nanoseconds per day (Jung et al 2020). That is 100,000 times smaller than a cell, and it would still take over 250,000 years to simulate a single second’s worth of behavior for this system on our current supercomputers. Not to mention that there are even finer levels of detail once we start accounting for quantum mechanics…
Needless to say, we won’t be simulating a whole cell at atomic detail anytime soon. The solution to this issue is to introduce sub-grid rules in your simulations that capture lower level phenomena you aren’t directly simulating. For instance, in simulating the weather, you may not be able to capture the formation of very small clouds, so modelers essentially end up adding those in manually when the conditions are right for their formation. In an example from my research modeling cell spreading during phagocytosis, we couldn’t possibly capture the detailed molecular interactions between antibodies and receptors allowing the immune cell to stick to a surface. So instead, we simply said if the cell gets close enough to the location of an IgG molecule, then binding occurs (Francis and Heinrich 2022).
The crucial point here is that introducing such rules to simulations is not a trivial task, and can often be done in many different ways (some of which can give very incorrect answers). This is where the “art of modeling” comes in. A scientist must decide the best way to formulate and implement such rules. In the example of immune cells binding to antibodies, for instance, we needed to determine some reasonable way to choose how close was “close enough” for the cell to bind. Rather than set this arbitrarily, we chose to match this to the magnitude of plasma membrane fluctuations (“wiggles” in the cell membrane that would effectively allow the cell to reach out and touch something a short distance away). We could have chosen some arbitrary length scale for this, but if we chose incorrectly, we wouldn’t have been able to see some of the effects we were looking for!
2. The theory-experiments feedback loop: In his book, Dr. Pontzen does an excellent job highlighting how computational and theoretical work in cosmology feeds into observational work (and vice versa). His prime example is dark matter; on its face, the statement that 85% of the mass in the universe is made up of some unknown type of matter that doesn’t interact with photons (“dark” matter) seems almost unbelievable. This means that the matter we know and love is outnumbered almost 6 to 1 as a whole. This finding involved many stages of interplay between theory and observations. Once the idea of dark matter was first suggested, theoretical physicists found that including it in simulations helped explain some of the remarkable large-scale structures we see in the universe as a whole (the “cosmic web”). Based on these simulations, further predictions could be made and tested experimentally. For instance, for these simulations to work, the mass of neutrinos had to be much smaller than originally thought, which was indeed confirmed via experiments.
The astounding agreement between simulations (left) and experiments (right) from Figure 11 in Hodgkin and Huxley’s seminal paper from 1952.
In biophysics, the situation is quite similar. Of course, historically, the way we best learned about biology was through a wide range of experiments. But this really started to change throughout the 20th century. Consider, for instance, the famous theoretical work by Hodgkin and Huxley in the 1950s, who used a set of differential equations to model action potentials in giant neurons from squid. They investigated what these equations would need to include to account for the experimental measurements, and predicted that there should be some mechanism to transport ions across the cell membrane in a voltage-sensitive manner. In the following decades, experimentalists began to discover that there were, in fact, proteins in the cell membrane that act as “channels” for ions and open and close in a voltage sensitive manner. Based on characterization of these proteins, theoretical biophysicists have then been able to predict how the behavior of these channels effects voltage changes at the whole cell level. It’s the classic theory-experiment feedback loop all over again!
3. Tradeoff between more detail vs. more simulations: If you recall from above, simulating most physical systems with full detail is simply not feasible. Indeed, there is always a tradeoff between the level of detail to include in a given simulation and the payoff you get from it. In his conversation with Sean Carroll, Dr. Pontzen points out, “You want to add layers of detail, but there's another interesting angle on this, which is as you add more detail, the simulation gets more powerful in certain ways, but in other ways it gets less powerful.” He points out that the ability to “turn certain features off” in a simulation (like removing black holes from the universe) relies on representing the universe in some crude, inexact way. After all, if we represented the universe exactly, it simply wouldn’t be possible to exclude black holes, since they are a real feature of the universe. In general, the down-to-earth question is how much detail you need to add to a model to answer some specific question. As a rule of thumb, the oft-quoted paraphrase of Einstein goes “Everything should be made as simple as possible, but no simpler”.
An example of a relatively simple model (A) simulated in a quite complex geometry (B-D) representing a small section of a neuron known as a dendritic spine. Figure 1 from Laughlin et al 2023.
We ask ourselves this question all the time in the work that I do (and this is, of course, connected my previous discussion of the “spherical cow” ideology). The level of detail we include in our models of cells varies from a couple of ordinary differential equations to large networks of partial differential equations solved within realistic cell geometries (see a recent software I helped develop, Spatial Modeling Algorithms for Reaction and Transport - SMART). Because many of the questions we want to answer rely on understanding the role of cell shape in signaling events within the cell, the more accuracy we can include in the geometry the better. However, the more we add, the longer the calculations take. Some of our recent simulations using realistic geometries at the whole-cell scale take up to a month to complete, which is tolerable, but still quite the commitment. Often, before going to that extreme, we start with simple geometries to understand the general principles of the system we are examining - spheres, cylinders, boxes, etc.
That said, there are many questions (both in cosmology and biophysics) that rely on our ability to include new levels of detail within simulations. Whether it be new computing technology allowing us to simulate more complicated systems, or new clever tricks using sub-grid rules as mentioned above, we have a long ways to go to answer our many questions about life, the universe, and everything.
References:
Francis, E. A. et al. Spatial modeling algorithms for reactions and transport (SMART) in biological cells. 2024.05.23.595604 Preprint at https://doi.org/10.1101/2024.05.23.595604 (2024).
Hodgkin, A. L. & Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117, 500–544 (1952).
Jung, J. et al. New parallel computing algorithm of molecular dynamics for extremely huge scale biological systems. Journal of Computational Chemistry 42, 231–241 (2021).
Laughlin, J. G. et al. SMART: Spatial Modeling Algorithms for Reactions and Transport. Journal of Open Source Software 8, 5580 (2023).
Vazza, F. & Feletti, A. The Quantitative Comparison Between the Neuronal Network and the Cosmic Web. Frontiers in Physics 8, (2020).